Error distributions – thermolib.error

class thermolib.error.ErrorArray(errors, axis=0)[source]

A class to represent an array of independent error distributions. This class is used to store the distributiosn for errors on the conditional probabilities, i.e. for each value of cv in p(q|cv) there is an error distribution. The error distribution on p(q|cv1) is assumed uncorrelated with that of p(q|cv2), but we still want to store the distribution for the errors for each cv value in one object.

Parameters:

  • errors (list of instances of Distribution) – list of error distirbutions to be stored

  • axis (int, optional, default=0) – the axis index along which the errors are stacked. Only two valid choices: 0 and -1

mean()[source]

Return the distribution mean for each element in the errors list

Returns:

mean of the distibution

Return type:

np.ndarray

nsigma_conf_int(nsigma)[source]

Compute the n-sigma confidence interval, i.e. 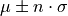\mu \pm n\cdot\sigma, for each element in the errors list

Returns:

mean of the distibution

Return type:

np.ndarray

sample(nsamples=None)[source]

Returns a number of random samples taken according to the error distribution for each element in the error list

Parameters:

nsamples (int or None, optional, default=None) – the number of samples returned. If None, a single sample will be returned and the shape of the return value will be identical to self.means and self.stds. If not None, the return value will have an additional dimension with size given by nsamples.

Returns:

multidimensional numpy array containing random samples for each element in self.errors. Shape of this array depends on nsamples, self.naxis and number of elements in self.errors.

Return type:

np.ndarray

std()[source]

Return the distribution standard deviation for each element in the errors list

Returns:

mean of the distibution

Return type:

np.ndarray

class thermolib.error.GaussianDistribution(means, stds)[source]

Implementation of a Gaussian distribution defined by its mean and standard deviation.

Parameters:

  • means (int, float or np.ndarray) – mean (or means if multidimensional) of the Gaussian distribution

  • stds (int, float or np.ndarray) – standard deviation (or standard deviations if multidimensional) of the Gaussian distribution

Raises:

  • ValueError – if means is not an integer, float or np.ndarray

  • AssertionError – if means and stds do not have same shape

copy()[source]

Return a hard copy of the Gaussian distribution

classmethod from_samples(samples)[source]

Defines a GaussianDistribution based on a population defined by the given samples. The routine will derive the mean and std from the population and use that to define the Gaussian Distribution.

Parameters:

samples (np.ndarray) – the samples that define the population

classmethod log_from_loggaussian(logdist, shift=0.0, scale=1.0)[source]

Define the Gaussian distribution of a variable 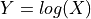Y=log(X) in which 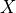X has a given LogGaussian distribution, potential after imposing a shift and rescaling.

Parameters:

  • logdist (LogGaussianDistribution) – the LogGaussian distribution of variable X in the expression above.

  • shift (float, optional, default=0.0) – shift to be applied to the mean upon conversion

  • scale (float, optional, default=1.0) – rescaling to be applied to the mean and std upon conversion

Raises:

AssertionError – if the given logdist is not an instance of LogGaussianDistribution

mean()[source]

Return the distribution mean

Returns:

mean of the distibution

Return type:

np.ndarray

nsigma_conf_int(nsigma)[source]

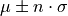
Compute the n-sigma confidence interval, i.e. \mu \pm n\cdot\sigma

Parameters:

nsigma (int, optional, default=2) – value of n in the above formula

print(fmt='%.3f', unit='au', do_scientific=False, nsigma=2)[source]

Routine to print the statistical properties of a scalar quantity.

Parameters:

  • fmt (str, optional, default='%.3f') – python string formatting for how to format floats (such as the mean and error). This argument is ignored if do_scientific is set tot True.

  • unit (str, optional, default='au') – unit in which to print the current quantity.

  • do_scientific (bool, optional, default=False) – use scientific formatting of floats

  • nsigma (int, optional, default=2) – print error bars as 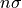n\sigma error bars. Hence, setting nsigma=2 will return error bars that are twice the standard deviation resulting from the error distribution.

sample(nsamples=None)[source]

Returns a number of random samples from the population defined by the Gaussian distribution

Parameters:

nsamples (int or None, optional, default=None) – the number of samples returned. If None, a single sample will be returned and the shape of the return value will be identical to self.means and self.stds. If not None, the return value will have an additional dimension with size given by nsamples.

Returns:

a (set of) random sample(s) from the population

Return type:

np.ndarray

set_ref(index=None, value=None)[source]

Set reference of distribution means by shifting them over an amount equal to -value or -self.means[index].

Parameters:

  • index (int, optional, default=None) – shift distribution means over an amount equal -self.means[index]. Ignored if set to None.

  • value (type consistent with population samples, optional, default=None) – shift distribution means over an amount equal to -value. Ignored if index is not None.

Raises:

ValueError – if both index and value are set to None

shift(ref)[source]

Shift the distribution means with the given ref.

Parameters:

ref (type consistent with means) – reference with which means will be shifted

std()[source]

Return the distribution standard deviation

Returns:

standard deviation of the distibution

Return type:

np.ndarray

class thermolib.error.LogGaussianDistribution(lmeans, lstds)[source]

Implementation of a Log-Gaussian distribution, i.e. variable X is Log-Gaussian with mean lmu and std lsigma if variable log(X) is Gaussian distributed with mean lmu and std lsigma.

Parameters:

  • lmeans – mean (or means if multidimensional) of the corresponding Gaussian distribution of log(X)

  • lstds – standard deviation (or standard deviations if multidimensional) of the corresponding Gaussian distribution of log(X)

Raises:

  • ValueError – if lmeans is not an integer, float or np.ndarray

  • AssertionError – if lmeans and lstds do not have same shape

copy()[source]

Return a hard copy of the LogGaussian distribution

classmethod exp_from_gaussian(gaussdist, shift=0.0, scale=1.0)[source]

Define the LogGaussian distribution of a variable 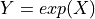Y=exp(X) in which 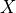X has a given Gaussian distribution, potential after imposing a shift and rescaling.

Parameters:

  • gaussdist (GaussianDistribution) – the Gaussian distribution of variable X in the expression above.

  • shift (float, optional, default=0.0) – shift to be applied to the mean upon conversion

  • scale (float, optional, default=1.0) – rescaling to be applied to the mean and std upon conversion

Raises:

AssertionError – if the given gaussdist is not an instance of GaussianDistribution

classmethod from_samples(samples)[source]

Defines a LogGaussianDistribution based on a population defined by the given samples. The routine will derive lmean and lstd from the log of the given population samples and use that to define the LogGaussian Distribution.

Parameters:

samples (np.ndarray) – the samples that define the population

mean()[source]

Return the distribution mean

Returns:

mean of the distibution

Return type:

np.ndarray

nsigma_conf_int(nsigma)[source]

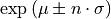
Compute the n-sigma confidence interval, i.e. \exp\left(\mu \pm n\cdot\sigma\right)

Parameters:

nsigma (int, optional, default=2) – value of n in the above formula

sample(nsamples=None)[source]

Returns a number of random samples from the population defined by the distribution

Parameters:

nsamples (int or None, optional, default=None) – the number of samples returned. If None, a single sample will be returned and the shape of the return value will be identical to self.means and self.stds. If not None, the return value will have an additional dimension with size given by nsamples.

Returns:

a (set of) random sample(s) from the population

Return type:

np.ndarray

set_ref(index=None, value=None)[source]

Set reference of distribution lmeans (NOT THE DISTRIBUTION MEANS!!) by shifting them over an amount equal to -value or -self.lmeans[index].

Parameters:

  • index (int, optional, default=None) – shift distribution lmeans over an amount equal -self.lmeans[index]. Ignored if set to None.

  • value (type consistent with population samples, optional, default=None) – shift distribution lmeans over an amount equal to -value. Ignored if index is not None.

Raises:

ValueError – if both index and value are set to None

shift(ref)[source]

Shift the distribution lmeans (NOT THE DISTRIBUTION MEAN!!) with the given ref.

Parameters:

ref (type consistent with lmeans) – reference with which lmeans will be shifted

std()[source]

Return the distribution standard deviation

Returns:

standard deviation of the distibution

Return type:

np.ndarray

class thermolib.error.MultiDistribution(shape, flattener=<thermolib.flatten.DummyFlattener object>)[source]

Abstract parent class for probability distributions of multidimensional stochastic properties used for error propagation. This class will explicitly account for correlation across the dimensions, as such it can be used to account for the correlation between the free energy at two different points in a FEP. Most of the routines here are implemented in the child classes.

Parameters:

  • shape (list of integers) – the dimensions of the property for which the distribution is stored

  • flattener (Flattener, optional, default=None) – The flattener encodes how to flatten the multidimensional properties stored in nD-arrays into a longer 1D-array for easiear error propagation. This flattener also allows to do the inverse transformation, i.e. deflatten the flattened 1D-array back to its original nD-array format.

corr(unflatten=True)[source]

Routine that will convert the covariance matrix computed with self.cov to a correlation matrix according to the formula

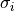Cor[i,j] &= \frac{Cov[i,j]}{\sigma_i \sigma_j}

in which \sigma_i is the standard deviation of the i-th quantity in the multidimensional stochastic property.

Parameters:

unflatten (bool, optional, default=True) – If True, return the correlation matrix in a shape equal to ‘the square’ of in the original dimensional shape. If False, return the correlation matrix as a flattened 2D array.

class thermolib.error.MultiGaussianDistribution(means, covariance, flattener=<thermolib.flatten.DummyFlattener object>)[source]

Implementation of a multivariate normal distribution for a given vector of means and a given covariance matrix

Parameters:

  • means (np.ndarray) – means of the multivariate normal distribution

  • covariance (np.ndarray with a dimension equal tot the square of means, i.e. if means.shape=(N,) then covariance.shape=(N,N) and if means.shape=(K,L) then covariance.shape=(K,L,K,L).) – covariance matrix of the multivariate normal distribution

  • flattener (Flattener, optional, default=DummyFlattener() indicating no flattening) – The flattener encodes how to flatten the multidimensional properties stored in nD-arrays into a longer 1D-array for easiear error propagation. This flattener also allows to do the inverse transformation, i.e. deflatten the flattened 1D-array back to its original nD-array format. Should be specified if len(means.shape)=1 because it represents a flattened 2D array (which also implies len(covariance.shape)=2 because it represents a flattened 4D array).

copy()[source]

Return a hard copy of the MultiGaussian distribution

cov(unflatten=True)[source]

Return the covariance matrix of the MultiGaussian distribution.

Parameters:

unflatten (bool, optional, default=True) – If True, return the covariance matrix in a shape equal to ‘the square’ of in the original dimensional shape. If False, return the covariance matrix as a flattened 2D array.

classmethod from_samples(samples, flattener=<thermolib.flatten.DummyFlattener object>, flattened=True)[source]

Defines a MultiGaussianDistribution based on a population defined by the given samples. The routine will derive the mean and std from the population and use that to define the Gaussian Distribution.

Parameters:

  • samples (np.ndarray) – the samples that define the population

  • flattened (bool, optional, default=False) –

    • If flattened is True, the given samples should be a 2D array in which a row represents all observations of a single variable and a column represents a single observation of all variables.

    • If flattened is False, then the the samples array is assumed to be 3 dimensional for which the first two dimensions represent a 2D index and the third index is the sample index. Therefore, the flattener will first be applied to flatten the 2D index into a 1D index and hence convert the samples to a 2D array of the same shape as required if the flattened argument is True.

Raises:

AssertionError – if the dimensions of samples array are invalid

classmethod log_from_loggaussian(logdist, shift=0.0, scale=1.0)[source]

Define the MultiGaussian distribution of a variable 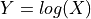Y=log(X) in which 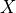X has a given MultiLogGaussian distribution, potential after imposing a shift and rescaling.

Parameters:

  • logdist (MultiLogGaussianDistribution) – the MultiLogGaussian distribution of variable X in the expression above.

  • shift (float, optional, default=0.0) – shift to be applied to the mean upon conversion

  • scale (float, optional, default=1.0) – rescaling to be applied to the mean and std upon conversion

Raises:

AssertionError – if logdist is not instance of MultiLogGaussianDistribution

mean(unflatten=True)[source]

Return the distribution mean

Parameters:

unflatten (bool, optional, default=True) – If True, return the distribution mean in the original dimensional shape. If False, return the distribution mean as a flattened 1D array.

Returns:

mean of the distibution

Return type:

np.ndarray

nsigma_conf_int(nsigma=2, unflatten=True)[source]

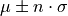
Compute the n-sigma confidence interval, i.e. \mu \pm n\cdot\sigma

Parameters:

  • nsigma (int, optional, default=2) – value of n in the above formula

  • unflatten (bool, optional, default=True) – If True, return the interval in the original dimensional shape. If False, return as a flattened 1D array.

plot_corr_matrix(fn=None, fig_size_inches=[8, 8], cmap='bwr', logscale=False, cvs=None, nticks=10, decimals=1)[source]

gMake a plot of the correlation matrix of the current multivariate Gaussian distribution

Parameters:

  • fn (_type_, optional, default=None) – file name to which figure will be saved. If None, figure will note be written to file.

  • fig_size_inches (list, optional, default=[8,8]) – [x,y]-dimensions of the figure in inches

  • cmap (str, optional, default='bwr') – color map to be used, see matplotlib documentation to see possibilities.

  • logscale (bool, optional, default=False) – plot correlation in logarithmic scale

  • cvs (np.ndarray, optional, default=None) – set x and y-tick labels to CV values given in cvs

  • nticks (int, optional, default=10) – number of ticks on x and y-axis. Only used when parameter cvs is given.

  • decimals (int, optional, default=1) – number of decimals to be shown in CV tick labels. Only used when parameter cvs is given.

sample(nsamples=None, unflatten=True)[source]

Returns a number of random samples from the population defined by the distribution

Parameters:

  • nsamples (int or None, optional, default=None) – the number of samples returned. If None, a single sample will be returned with a shape depending on whether or not it is flattened (see parameter unflatten). If not None, the return value will have an additional dimension with size given by nsamples.

  • unflatten (bool, optional, default=True) – If True, return each distribution sample in the original dimensional shape. If False, return each sample as a flattened 1D array.

Returns:

a (set of) random sample(s) from the population

Return type:

np.ndarray whose dimension depend on the nsamples and unflatten keyword values. If nsamples is None, a single sample is returned whose shape depends on whether or not it is flattened (see parameter unflatten). If nsamples is not None, the return value will have an additinal dimension with size given by nsamples.

set_ref(index=None, value=None)[source]

Set reference of distribution means by shifting them over an amount equal to -value or -self.means[index].

Parameters:

  • index (tuple|list, optional, default=None) – shift distribution means over an amount equal -self.means[index]. Ignored if set to None.

  • value (type consistent with population samples, optional, default=None) – shift distribution means over an amount equal to -value. Ignored if index is not None.

Raises:

ValueError – if both index and value are set to None

std(unflatten=True)[source]

Return the distribution standard deviation (std)

Parameters:

unflatten (bool, optional, default=True) – If True, return the distribution std in the original dimensional shape. If False, return the distribution std as a flattened 1D array.

Returns:

standard deviation of the distibution

Return type:

np.ndarray

class thermolib.error.MultiLogGaussianDistribution(lmeans, lcovariance, flattener=<thermolib.flatten.DummyFlattener object>)[source]

Implementation of a multivariate log-normal distribution for a given vector of means and a given covariance matrix

Parameters:

  • means (np.ndarray) – lmeans of the multivariate log-normal distribution, i.e. means of the underlying normal distribution of log(X)

  • covariance (np.ndarray with a dimension equal tot the square of means, i.e. if means.shape=(N,) then covariance.shape=(N,N) and if means.shape=(K,L) then covariance.shape=(K,L,K,L).) – lcovariance matrix of the multivariate log-normal distribution, i.e. covariance matrix of the underlying normal distribution of log(X)

  • flattener (Flattener, optional, default=DummyFlattener() indicating no flattening) – The flattener encodes how to flatten the multidimensional properties stored in nD-arrays into a longer 1D-array for easiear error propagation. This flattener also allows to do the inverse transformation, i.e. deflatten the flattened 1D-array back to its original nD-array format. Should be specified if len(means.shape)=1 because it represents a flattened 2D array (which also implies len(covariance.shape)=2 because it represents a flattened 4D array).

copy()[source]

Return a hard copy of the MultiLogGaussian distribution

cov(unflatten=True)[source]

Compute and and return the covariance matrix of the MultiLogGaussian distribution.

Parameters:

unflatten (bool, optional, default=True) – If True, return the covariance matrix in a shape equal to ‘the square’ of in the original dimensional shape. If False, return the covariance matrix as a flattened 2D array.

classmethod exp_from_gaussian(gaussdist, shift=0.0, scale=1.0)[source]

Define the MultiLogGaussian distribution of a variable 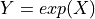Y=exp(X) in which 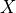X has a given MultiGaussian distribution, potential after imposing a shift and rescaling.

Parameters:

  • gaussdist (GaussianDistribution) – the Gaussian distribution of variable X in the expression above.

  • shift (float, optional, default=0.0) – shift to be applied to the mean upon conversion

  • scale (float, optional, default=1.0) – rescaling to be applied to the mean and std upon conversion

Raises:

AssertionError – if the given gaussdist is not an instance of MultiGaussianDistribution

classmethod from_samples(samples, flattener=<thermolib.flatten.DummyFlattener object>, flattened=True)[source]

Defines a MultiLogGaussianDistribution based on a population defined by the given samples. The routine will derive the lmean and lcovariance from the population and use that to define the MultiLogGaussian Distribution.

Parameters:

  • samples (np.ndarray) – the samples that define the population

  • flattened (bool, optional, default=False) –

    • If flattened is True, the given samples should be a 2D array in which a row represents all observations of a single variable and a column represents a single observation of all variables.

    • If flattened is False, then the the samples array is assumed to be 3 dimensional for which the first two dimensions represent a 2D index and the third index is the sample index. Therefore, the flattener will first be applied to flatten the 2D index into a 1D index and hence convert the samples to a 2D array of the same shape as required if the flattened argument is True.

Raises:

AssertionError – if the dimensions of samples array are invalid

mean(unflatten=True)[source]

Return the distribution mean

Parameters:

unflatten (bool, optional, default=True) – If True, return the distribution mean in the original dimensional shape. If False, return the distribution mean as a flattened 1D array.

Returns:

mean of the distibution

Return type:

np.ndarray

nsigma_conf_int(nsigma, unflatten=True)[source]

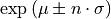
Compute the n-sigma confidence interval, i.e. \exp\left(\mu \pm n\cdot\sigma\right)

Parameters:

  • nsigma (int, optional, default=2) – value of n in the above formula

  • unflatten (bool, optional, default=True) – If True, return the interval in the original dimensional shape. If False, return as a flattened 1D array.

plot_corr_matrix(fn=None, fig_size_inches=[8, 8], cmap='bwr', logscale=False, cvs=None, nticks=10, decimals=1)[source]

gMake a plot of the correlation matrix of the current multivariate Gaussian distribution

Parameters:

  • fn (_type_, optional, default=None) – file name to which figure will be saved. If None, figure will note be written to file.

  • fig_size_inches (list, optional, default=[8,8]) – [x,y]-dimensions of the figure in inches

  • cmap (str, optional, default='bwr') –

    color map to be used, see matplotlib documentation to see possibilities.

  • logscale (bool, optional, default=False) – plot correlation in logarithmic scale

  • cvs (np.ndarray, optional, default=None) – set x and y-tick labels to CV values given in cvs

  • nticks (int, optional, default=10) – number of ticks on x and y-axis. Only used when parameter cvs is given.

  • decimals (int, optional, default=1) – number of decimals to be shown in CV tick labels. Only used when parameter cvs is given.

sample(nsamples=None, unflatten=True)[source]

Returns a number of random samples from the population defined by the distribution

Parameters:

  • nsamples (int or None, optional, default=None) – the number of samples returned. If None, a single sample will be returned with a shape depending on whether or not it is flattened (see parameter unflatten). If not None, the return value will have an additional dimension with size given by nsamples.

  • unflatten (bool, optional, default=True) – If True, return each distribution sample in the original dimensional shape. If False, return each sample as a flattened 1D array.

Returns:

a (set of) random sample(s) from the population

Return type:

np.ndarray whose dimension depend on the nsamples and unflatten keyword values. If nsamples is None, a single sample is returned whose shape depends on whether or not it is flattened (see parameter unflatten). If nsamples is not None, the return value will have an additinal dimension with size given by nsamples.

std(unflatten=True)[source]

Return the distribution standard deviation (std)

Parameters:

unflatten (bool, optional, default=True) – If True, return the distribution std in the original dimensional shape. If False, return the distribution std as a flattened 1D array.

Returns:

standard deviation of the distibution

Return type:

np.ndarray

class thermolib.error.Propagator(ncycles=50, target_distribution=<class 'thermolib.error.GaussianDistribution'>, flattener=<thermolib.flatten.DummyFlattener object>, samples_are_flattened=False, verbose=False)[source]

A class to propagate the error distribution on a set of arguments towards the error distribution on a given function of those arguments. This routine uses the sample routine of each of its distrubution arguments, meaning that the resulting error is stochastic (will not give the same repeated result).

Parameters:

  • ncycles (int, optional, default given by value of global variable ncycles_default) – the number of cycles for which a random sample is taken for each argument and corresponding function value is computed.

  • target_distribution (child class of Distribution, optional, default=GaussianDistribution) – the type of distribution to be used for the error of the function value. Can be overwritten in the get_distribution routine.

  • flattener (instance of child class of Flattener, optional, default=DummyFlattener()) – Flattener to be parsed to the error distribution of the function value. Can be overwritten in the get_distribution routine.

  • samples_are_flattened (bool, optional, default=False) – whether or not the samples generated by gen_args_samples (and hence the sample routine of the arguments) are flattened. Can be overwritten in the get_distribution routine.

  • verbose (bool, optional, default=False) – If True, increase verbosity of the propagator logging

calc_fun_values(fun)[source]

Routine to compute the function value for each set of random samples stored for the arguments during execution of the gen_args_samples routine.

Parameters:

fun (callable) – function f for which the error needs to be computed

gen_args_samples(*args)[source]

Routine that will generate random samples for each of the given arguments. The total number of samples per argument is defined in self.ncycles.

Parameters:

args (list of distributions) – list of arguments of the function for which the error needs to be computed

get_distribution(target_distribution=None, flattener=None, samples_are_flattened=None)[source]

Routine to construct the error distribution of the function value from a population generated by the routines gen_args_samples and calc_fun_values. For more info on arguments target_distribution, flattener or samples_are_flattened, see documentation in the initializer. Only if such an argument is explicitly specified (i.e. is not None), will it be overwritten with the given value.

Returns:

Distribution of the function value

Return type:

determined by parameter target_distribution

reset(target_distribution=None, flattener=None, samples_are_flattened=None)[source]

Reinitialize argsamples for future reuse. For more info on arguments target_distribution, flattener or samples_are_flattened, see documentation in the initializer. Only if such an argument is explicitly specified (i.e. is not None), will it be overwritten with the given value.

class thermolib.error.SampleDistribution(samples)[source]

Define the distribution by explicitly supplying it with a population of samples. All statistical properties will be derived from this population.

Parameters:

samples (np.ndarray) – the samples that define the population

classmethod from_samples(samples)[source]

Defines the current SampleDistribution based on a population defined by the given samples. A trivial routine for the current class, but implemented for completeness of Distribution parent class.

Parameters:

samples (np.ndarray) – the samples that define the population

mean()[source]

Return the distribution mean

Returns:

mean of the distibution

Return type:

np.ndarray

sample()[source]

Returns a random sample from the population given at initialization

Returns:

a random sample from the population

Return type:

np.ndarray or float

set_ref(index=None, value=None)[source]

Set reference of population samples by shifting all population samples over an amount equal to -value.

Parameters:

  • index – invalid keyword for SampleDistribution. Only valid value is None.

  • value (type consistent with population samples, optional, default=None) – old population value that will become new reference (i.e. become zero)

Raises:

  • AssertionError – if index is not None

  • AssertionError – if value is None

shift(ref)[source]

Shift all samples in the population with the given ref.

Parameters:

ref (type consistent with a sample from the population) – reference with which each sample will be shifted

std()[source]

Return the distribution standard deviation

Returns:

standard deviation of the distibution

Return type:

np.ndarray